L'ancoraggio in numeri (1)

Qualche numero su come si comporta una linea d'ancoraggio: prendo come caso iniziale una catena da 10, come quella che ho in barca. 
Le caratteristiche di una linea possono venir studiate tramite le equazioni caratteristiche della catenaria, una catena in tensione infatti si dispone come per esempio un filo appeso ai due lati, solo che la catena ha un estremo appoggiato sul fondo. 

Una domanda classica è "quale rapporto fra lunghezza di catena filata e la profondità?". Chiaro la profondità viene contata a partire dal musone.

Ognuno ha il suo modo di fare quindi non c'è una risposta univoca, si possono invece fare dei paragoni fra ancoraggi in profondità differenti.

Consideriamo come situazione limite il momento in cui l'ultimo anello di catena si solleva dal fondo del mare, cioè quando il profilo inferiore della catenaria è tangente al fondo del mare: la barca tira tira sulla catena fino a quando l'ultimo anello di catena sta per sollevarsi dal fondo, li' misuro il carico.

1. A parità di carico limite, ancorare in una profondità maggiore permette di utilizzare un rapporto catena/profondità inferiore a quello necessario con una profondità minore.

Il carico sulla catena è proporzionale (per un fattore dipendente dal peso lineare della catena) al quadrato della lunghezza di catena diviso per la profondità. A parità di carico, all'aumentare della profondità quindi la catena deve aumentare proporzionalmente di meno.
In cifre:

A parità di tensione, ponendo calumo per esempio 5:1 (i carichi sono al netto di una costante di proporzionalità):

.con profondità =1, lunghezza catena = 5, carico = 25
.con profondità =2, lunghezza catena =10, carico = 100/2=50 --> stesso calumo, doppio del carico

Per sapere che calumo usare con profondità =2 per avere gli stessi 25 di carico della profondità 1 --> 25 = catena^2/profondità da cui catena= sqrt(50) = circa 7
calumo/profondità =7/2=3.5

Quindi a parità di carico, una profondità uguale a 2 e calumo 3.5:1 sono equivalenti a profondità  1 e calumo 5:1




Un esempio pratico, due profondità 5 e 10m. Calcolo della forza limite che "solleva l'ultimo anello di catena" per linea omogenea di catena 10mm.

Profondità 5m, calumo 25m --> 122daN
Per avere gli stessi 122dan, con Profondità 10m posso mettere solo 36m di catena, rapporto 3.6/1.

In entrambi i casi la catena è sottoposta alla stessa trazione, l'ultimo anello attaccato all'ancora si sta appena sollevando dal suolo, l'angolo di trazione quindi è 0° per definizione.

Per riassumere un po', un paio di figure

Nella prima, un grafico con in ordinata la profondità e in ascissa i metri di catena necessari per avere una trazione sull'ancora orizzontale; le varie curve rappresentano valori di carico crescenti, la curva 5 rappresenta un carico 10 volte superiore alla curva 1. Si vede bene come all'aumentare della profondità, la lunghezza di catena necessaria aumenta meno che proporzionalmente. In particolare vi sono differenze molto vistose per i primi  5-10m di profondità.


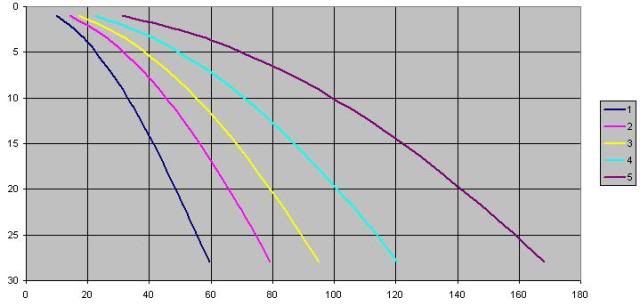
In questa figura invece viene indicato in ascissa il rapporto (lunghezza di catena : profondità) necessario per mantenere l'angolo sull'ancora orizzontale, a seconda dei vari carichi (le varie curve, anche qui la 5 rappresenta un carico 10 volte superiore alla 1).
Un'altra cosa mostrata dalla figura, andare oltre un rapporto catena/profondità di 8-9 praticamente non porta più vantaggi apprezzabili, specie a profondità di 5-10m



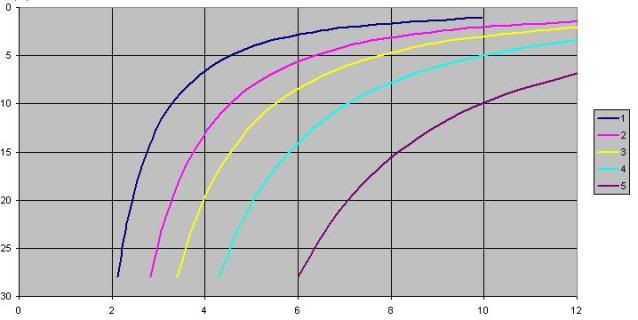
qui si vede meglio: le curve sono per carichi da 100 a 500, da sinistra a destra.

Ogni curva rappresenta lo "scope" (rapporto lunghezza catena: profondità) necessario a quella determinata profondità per sollevare l'ultimo anello di catena con il carico rappresentato dalla curva.
Esempio, curva gialla nel mezzo (corrispondente a 300daN di carico) --> per tenere la catenaria tangente al suolo in 5m di profondità (linea orizzontale 5) ho bisogno di almeno 8 di scope (linea verticale 8). 

Per questo tipo di carichi quindi si vede che in 5m di profondità con uno scope fra 6 e 10 si tiene la linea tangente; per 10m di profondità con gli stessi carichi basta uno scope diciamo fra 4 e 7.
*Con questi carichi* andare al di là di questi scope ha un'utilità che decresce molto rapidamente.




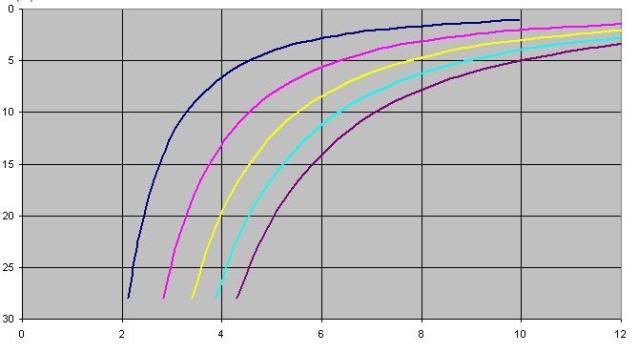
Cosa succede quando il carico sulla catena aumenta ?  Quale angolo comincia a fare la catena con il fondo ?
Con le due linee, 25m in 5m di profondità, e 36m in 10m di profondità, supponiamo arrivi un rafficone che raddoppia la forza aerodinamica --> 250daN, che diventa un nuovo parametro della stessa equazione che stavolta risolviamo per l'angolo della tangente inferiore alla catenaria.

A parità di trazione 250daN, ottengo

Linea profondità 5m con catena 25m --> 6°
Linea prof 10m con catena 36m --> 7.5°

1.5° di differenza... 

Se si ancorasse con una linea tutta tessile chiaro gli angoli sarebbero molto molto maggiori.

Supponiamo qualcosa di più realistico rispetto al calumo 3.6/1 che magari uno non mette se si aspetta il rafficone che raddoppia, sempre per vedere la differenza fra proporzioni di calumo diverse a seconda della profondità:

1. Profondità 5m, 35m calumo, 7:1 --> forza limite 250 daN
2. Profondità 10m, 50m calumo, 5:1 --> forza limite 250 daN

rafficone, forza esercitata 500daN, cosa succede all'angolo ?

1. Caso 5m/35m/7:1 --> angolo 4.2°
2. Caso 10m/50m/5:1 --> angolo 5.9°

la differenza rimane più o meno costante, 1.7°



Il rapporto calumo:profondità viceversa comincia a giocare molto di più quando ci si avvicina alla lunghezza per definizione limitata di catena che uno ha in barca: supponendo 70m totali in entrambi i casi

con 5m di profondità, porto il calumo tangente con circa 1000daN. Siamo in un rapporto 14:1...

con 10m di profondità, porto il calumo tangente con circa 500daN, la metà; siamo a un rapporto 7:1

Continuiamo in quest'ultimo caso:
Poniamo 5m di profondità, 70m di calumo, forza 1000daN. Per definizione l'angolo è 0°.
Che angolo avro' all'ancora con stessi 70m catena, stessa forza e 10m di profondità: dopo un breve calcolo 4.2°


Aumentando ancora i carichi, siamo in condizioni alle quali applichiamo un'analisi statica, ma che per entità dei carichi vengono raggiunte solo in situazioni dinamiche, dove quindi molti altri fattori entrano in conto nella determinazione del carico massimo sulla linea (composizione della linea, comportamento dinamico della barca, moto ondoso, eccetera), il rapporto catena:profondità quindi tenderà a diventare meno rilevante.

Segue, per chi proprio non si fosse ancora addormentato.